Mathematical Playtime 4

Before reading this journal I recommend my very dear readers to repeat the short articles 2 and 3 in my Chaotic series of fractal articles, especially because there been a typos, newly corrected, where the base and the exponent until now been confused I also recommend you to check out the short article 9 in the above mentioned Chaotic series.

Special preperiodic cycles and acupuncture points
In part 1 we learned that rationals with even denominators are preperiodic under doubling. We have seen one example on that,
1/6, 1/3, 2/3, it’s shift map being 001. Now there are some special even numbers in the denominators, which are very special. Those even numbers are 2, 4, 8, 16, etc, expressed as exponentials of 2, as 2^1, 2^2, 2^3, 2^4, etc Example; 3/4, 1/8, and 5/16 of a whole turn. Let’s take the last one and perform the angle doubling;

5/16 -> 10/16 = 5/8 -> 10/8 – 1 = 5/4 – 1 = 5/4 – 4/4 = 1/4 -> 2/4 = 1/2 -> 2/2 – 1 = 1 – 1 = 0 -> 0 etc.
That is the orbit;
5/16 -> 5/8 -> 1/4 -> 1/2 -> 0.

We see they are preperiodic to period 1, or in other words, they go to a fixpoint.
Question: What’s the special with these angles?
Answer: They are exactly those angles, together with the angle 0, that in our four illustrations,


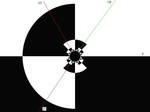
to the previous journal, as well in every image were binary decomposition is used, are denoted by the borderlines between the black and white areas that radiates from the circle, or the fractal. For those spots from where those lines radiates I, in my chaotic series, have invented the term “acupuncture points”. More about those acupuncture points can be read in especially article 3 and article 9 in this series.

Angle doubling is the same as squaring
In this playtime series we have seen that the angle doubling and the shift map is the same operation. Moreover, the angle doubling is essentially the same operation as the dynamical process z -> z^2 Regarding this, take a look at Iteration in the Complex Number Plane As I myself am only a wannabe mathematician (that is I am NOT a mathematician at all), no evidence will be shown. However note that complex arithmetic operations most often affect the angles of the complex numbers. It’s easy to see that squaring complex numbers that are situated on a radius of one, that is they are situated on the Julia set for the dynamical process z -> z^2, are complete identical with angle doubling. If we take z = i (at the very top of the circle) we obtain the orbit;

i -> -1 -> 1 -> 1 etc.

It’s easy to see that z = i is situated at the angle 1/4, z =  -1 at 1/2, z = 1 at 1 or 0 of a whole turn. Under angle doubling we have;

1/4 -> 1/2 -> 0 -> 0 etc.

Performing shift map is only meaningful until we reach the radial borderline between the black and white fields. That’s because we thereafter at the same time have both “half 0” and “half 1”.

In the same way starting with z = -i at the very bottom of the circle gives the orbit;

-i -> -1 -> 1 -> 1 etc.

Which regarded as angle doubling gives;

3/4 -> 1/2 -> 0 -> 0 etc.

This can clearly be seen if you look at the illustration in Iteration in the Complex Number Plane. In this way as the radial border lines between the black and white section point out the points on the circle that are preperiodic to the fixpoint z = 1 + 0i. In the same way it’s also easy to check out were periodic points, and it’s preperiodics, of any period is situated on the circle. In the illustrations to this journal, all 2-periodic (as well as one of its preperiodics) and 3-periodic points are pointed out at the endpoints of the lines that denote these periodic (and preperiodic) angles. That is, these points on the circle have these periods under the dynamical process z -> z^2 However checking out periodic points and its preperiodics on the circle is much more difficult using the dynamical process z -> z^2 So using angle doubling is a wonderful tool for studying the dynamics of the process z -> z^2.

There are also orbits that are entirely chaotic, that is never in infinity returning to the same spot on the circle. They are, regarded as angles measured as fractions of a whole turn, represented by irrational numbers. That is they can NOT be brought into the form p/q where p and q are integers.

Angle doubling, shift map, are not only wonderful tools for studying the Julia set for z -> z^2, but for ALL quadratic Julia sets, that is z -> z^2 + c, and in fact also for the Mandelbrot set The evidence for all this is beyond my mathematical horizon. However we have to trust the great mathematicians The great mathematicians can explain much (or maybe most) of the facilities of the Mandelbrot set by external rays drown from far distance coming perpendicular to the level sets and finally landing at the border of the Mandelbrot set. The angles we are talking about are the angles these rays have far from the set when they are stretched out.

With these words our Mathematical Playtime series has come to the end. It is meant to be a “reference library” for me (and of course YOU) to refer back to. The next occasion for this will probably be for a journal, containing many illustrations, dealing with how we, starting with the shift map, can identify where so called “hyperbolic components” with a certain period of the Mandelbrot set are located and how many they are I have not even started this “ project”, but beware, I have it in my head

…And beware, for Cubics there are three symbols (0, 1, and 2) in the shift map